注意：

  • 高精度！

实现树的Prufer编码

Prufer编码是用另外一种形式来描述一棵树，这棵树是无根树，它可以和无根树之间形成一一对应关系。已知树，如何求Prufer编码？
首先选这棵树叶子中编号最小的点，将这个点删除，并且把它的邻接点加入一个数组中，例如第一个删除的节点为$1$，并且把$5$加入数组中。删除节点后形成一棵新的树，再在新树中删除最小的节点，并且把邻接点加入数组中，这样重复以上步骤，直到树中最后剩余两个点的时候终止操作。这时候数组中的便是Prufer编码。

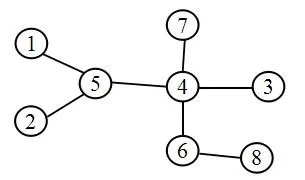
例如上图是一棵无根树，这棵树的Prufer编码为$(5,5,4,4,4,6)$。

将Prufer编码还原为一棵树

假如Prufer编码为$(a_1,a_2,a_3,\cdots a_{n-2})$在上述数组中，在数组最后加入$n$这个值，这样便形成了数组中包含$n-1$个节点，例如上述为$(5,5,4,4,4,6,8)$。
然后取不在数组中的最小值为$b_1$，则$b_1$与$a_1$是邻接点，在数组中删除$a_1$，再在剩下的数中选取不为$b_1$，且不在数组中的最小值为$b_2$，则$b_2$与$a_2$是邻接点，这样依次循环下去直到结束，这样便形成了一棵树。

Prufer编码的性质

Cayley 定理：不同的$n$节点标号树的数量为$n^{n-2}$。
任意一棵$n$节点的树都可唯一的用长度为$n-2$的Prufer编码表示；度数为$m$的节点的序号在Prufer编码中出现的次数为$m-1$；

例题：[HNOI2008]明明的烦恼

题目描述

自从明明学了树的结构，就对奇怪的树产生了兴趣……给出标号为$1$到$N$的点，以及某些点最终的度数，允许在任意两点间连线，可产生多少棵度数满足要求的树？

输入格式

第一行为$N(0\lt N\le 1000)$，接下来$N$行，第$i+1$行给出第$i$个节点的度数$D_i$，如果对度数不要求，则输入-1

输出格式

一个整数,表示不同的满足要求的树的个数，无解输出0

输入

1
2
3
4
3
1
-1
-1

输出

1
2

说明/提示

两棵树分别为1-2-3;1-3-2

题目分析

该题需要将树转化为prufer编码：
$n$为树的节点数，$d_i$为各节点的度数，$m$为无限制度数的节点数。
则有度数的点出现次数为：$\begin{split}tot=\sum_{i=1}^n (d_i-1)\end{split}$，因为度数为$d_i$的点出现了$d_i-1$次
所以要求在$n-2$大小的数组中插入$tot$个序号，共有$\begin{split}C_{n-2}^{tot}\end{split}$种插法；
在$tot$个序号排列中，插第一个节点的方法有$\begin{split}C_{tot}^{d_1-1}\end{split}$种插法；
插第二个节点的方法有$\begin{split}C_{tot}^{d_2-1}\end{split}$种插法；
…………
另外还有$m$个节点无度数限制，所以它们可任意排列在剩余的$n-2-tot$的空间中，排列方法总数为$\begin{split}m^{n-2-tot}\end{split}$
根据乘法原理：

$\begin{split} ans&=C_{n-2}^{tot}\cdot C_{tot}^{d_1-1}\cdot C_{tot-(d_1-1)}^{d_2-1}\cdots C_{d_n-1}^{d_n-1}\cdot m^{n-2-tot}\\ &=\frac{(n-2)!}{(n-2-tot)!\cdot tot!}\cdot \frac{tot!}{(d_1-1)!\cdot (tot-d_1+1)!}\cdots \frac{(d_n-1)!}{(d_n-1)!\cdot 0!}\cdot m^{n-2-tot}\\ &=\frac{(n-2)!\cdot m^{n-2-tot}}{(n-2-tot)!\cdot (d_1-1)!\cdot (d_2-1)!\cdots(d_n-1)!} \end {split}$

然后就要高精度了……但高精度除法太麻烦了，显而易见的排列组合一定是整数，所以可以进行质因数分解，再做一下相加减。
关于 $n!$质因数分解有两种方法，第一种暴力分解，这里着重讲第二种。
若$p$为素数，则$n!$可分解为一个数$\cdot p^x$，其中$\begin{split} x=\left\lfloor\frac np\right\rfloor+\left\lfloor\frac n{p^2}\right\rfloor+\cdots+\left\lfloor\frac n{p^t}\right\rfloor\end{split}$且$\begin{split}p^t\lt n\end{split}$
所以$\begin {split} n!=p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}\cdots p_m^{x_m}\qquad(p_m\lt n)\end{split}$
代码详见Code

模板题

讲义下载