由于内容过长、公式较多，暂时将内容隐藏，请公式恐惧症们做好心理准备。

Problem

Description

轮状病毒有很多变种，所有轮状病毒的变种都是从一个轮状基产生的。一个 $N$ 轮状基由圆环上 $N$ 个不同的基原子
和圆心处一个核原子构成的，$2$ 个原子之间的边表示这 $2$ 个原子之间的信息通道。如下图所示

$N$ 轮状病毒的产生规律是在一个 $N$ 轮状基中删去若干条边，使得各原子之间有唯一的信息通道，例如共有 $16$ 个不
同的 $3$ 轮状病毒，如下图所示：

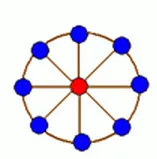
现给定 $N (N\le 100)$，编程计算有多少个不同的 $N$ 轮状病毒

Input

第一行有 $1$ 个正整数 $N$

Output

计算出的不同的 $N$ 轮状病毒数输出

Sample Input

1
3

Sample Output

1
16

法一: 行列式

转载自 vfleaking，题解备份
对于新手还是建议去看看基尔霍夫矩阵，这一篇 论文 挺不错的
用基尔霍夫矩阵使用高斯消元解行列式，时间复杂度 $O(n^3)$ 似乎可以 AC。
首先行列式有很多性质，第 $a$ 行 $\times k$ 加到第 $b$ 行上去，行列式的值不变。
三角行列式的值等于对角线元素之积。
第 $a$ 行与第 $b$ 行互换，行列式的值取反。
常数 $\times$ 行列式，可以把常数乘到某一行里去。
如果你行列式不是很熟，建议先搜搜行列式～不然下面会看晕～

其实如果你仔细观察矩阵，可以发现它是这样的：（消去了病毒中央）

$\begin{vmatrix} 3 &-1 &0 &0 &\cdots &0 &0 &0 &-1\\ -1 &3 &-1 &0 &\cdots &0 &0 &0 &0\\ 0 &-1 &3 &-1 &\cdots &0 &0 &0 &0\\ 0 &0 &-1 &3 &\cdots &0 &0 &0 &0\\ 0 &0 &0 &-1 &\cdots &0 &0 &0 &0\\ \vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots &\vdots &\vdots\\ 0 &0 &0 &0 &\cdots &3 &-1 &0 &0\\ 0 &0 &0 &0 &\cdots &-1 &3 &-1 &0\\ 0 &0 &0 &0 &\cdots &0 &-1 &3 &-1\\ -1 &0 &0 &0 &\cdots &0 &0 &-1 &3 \end{vmatrix}$

那么我们现在对行列式进行变换，我们把第 $1$ 行与第 $2$ 行交换，再把第 $2$ 行与第 $3$ 行交换……，再把第 $n-1$ 行与第 $n$ 行变换，得到新的行列式：

$\begin{vmatrix} -1 &3 &-1 &0 &\cdots &0 &0 &0 &0\\ 0 &-1 &3 &-1 &\cdots &0 &0 &0 &0\\ 0 &0 &-1 &3 &\cdots &0 &0 &0 &0\\ 0 &0 &0 &-1 &\cdots &0 &0 &0 &0\\ \vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots &\vdots &\vdots\\ 0 &0 &0 &0 &\cdots &3 &-1 &0 &0\\ 0 &0 &0 &0 &\cdots &-1 &3 &-1 &0\\ 0 &0 &0 &0 &\cdots &0 &-1 &3 &-1\\ -1 &0 &0 &0 &\cdots &0 &0 &-1 &3\\ 3 &-1 &0 &0 &\cdots &0 &0 &0 &-1 \end{vmatrix}$

这个行列式跟一开始的那个行列式的值不一定相等。
因为我们是通过 $n-1$ 次交换行的操作得到的，
为了说话方便我们称一开始的行列式为 $A$，上面刚写的行列式为 $B$
那么由行列式性质得：$A=(-1)^{n-1}\cdot B$
现在就可以正大光明地处理 $B$ 了～

利用行列式性质，来手算这个行列式。之所以刚才有那么一步，就是为了方便手算。
因为观察 $B$ 矩阵，发现就只剩下左下角的 $-1$、$3$、$-1$ 三个倒霉了。

$\begin{matrix} \text{倒数第二行：} &-1 &0 &0 &0 &\cdots &0 &0 &-1 &3\\ \text{用第一行的：} &-1 &3 &-1 &0 &\cdots &0 &0 &0 &0\\ \text{乘以}-1\text{ 来消：} &0 &-3 &1 &0 &\cdots &0 &0 &-1 &3\\ \text{再用第二行：} &0 &-1 &3 &-1 &\cdots &0 &0 &0 &0\\ \text{乘以}-3\text{ 来消：} &0 &0 &-8 &3 &\cdots &0 &0 &-1 &3 \end{matrix}$

这样就有了初步感觉了～

现在把这个过程一般化：

$\begin{matrix} \text{第 }k\text{ 个和第 }k+1\text{ 个：} &0 &0 &\cdots &F(k) &G(k) &0 &0 &\cdots &-1 &3\\ \text{总能找到上面的某一行} &0 &0 &\cdots &-1\quad &3~~~ &-1 &0 &\cdots &0 &0\\ \text{乘以 }F(k)\text{ 来消：} &0 &0 &\cdots &0 &F(k+1) &G(k+1) &0 &\cdots &-1 &3\\ \end{matrix}$

于是得到：

$\begin{cases} F(k+1)=G(k)+3F(k)\\ G(k+1)=-F(k) \end{cases}$

整合一下：$F(k+1)=3F(k)-F(k-1)$
从初始的行和消了一次之后的行中取得边界条件：$F(1)=-1,F(2)=-3$
最终一定会变为下面这种情况：

$\begin{matrix} \text{倒数第二行：} &0 &0 &0 &0 &\cdots &F(n-3) &G(n-3) &-1 &3\\ \text{用倒数第四行：} &0 &0 &0 &0 &\cdots &-1 &3 &-1 &0\\ \text{乘以 }F(n - 3)\text{ 来消：} &0 &0 &0 &0 &\cdots &0 &F(n-2) &G(n-2)-1 &3\\ \text{用倒数第三行：} &0 &0 &0 &0 &\cdots &0 &-1 &3 &-1\\ \text{乘以 }F(n - 2)\text{ 来消：} &0 &0 &0 &0 &\cdots &0 &0 &F(n-1)-1 &G(n-1)+3 \end{matrix}$

好现在搞定了倒数第二行，来看看成果：$(f=F(n-1)-1,g=G(n-1)+3)$

$\begin{vmatrix} -1 &3 &-1 &0 &\cdots &0 &0 &0 &0\\ 0 &-1 &3 &-1 &\cdots &0 &0 &0 &0\\ 0 &0 &-1 &3 &\cdots &0 &0 &0 &0\\ 0 &0 &0 &-1 &\cdots &0 &0 &0 &0\\ \vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots &\vdots &\vdots\\ 0 &0 &0 &0 &\cdots &3 &-1 &0 &0\\ 0 &0 &0 &0 &\cdots &-1 &3 &-1 &0\\ 0 &0 &0 &0 &\cdots &0 &-1 &3 &-1\\ 0 &0 &0 &0 &\cdots &0 &0 &f &g\\ 3 &-1 &0 &0 &\cdots &0 &0 &0 &-1 \end{vmatrix}$

好，现在来搞倒数第一行。
和倒数第二行的方法是类似的。
再设函数 $H(k)$ 和 $I(k)$，意义与 $F(k)$、$G(k)$ 类似,得：

$\begin{cases} H(k+1)=I(k)+3H(k)\\ I(k+1)=-H(k) \end{cases}$

其实跟 $F$、$G$的递推式是一样的我会乱说？$H(k+1)=3H(k)-H(k-1)$
边界条件是：$H(1)=3,H(2)=8$
最后使劲搞一搞，倒数第一行就成了：

$\begin{matrix} 0 &0 &0 &0 &0 &\cdots &0 &0 &H(n - 1) &I(n - 1)-1 \end{matrix}$

再来看成果：$(h=H(n-1),i=I(n-1)-1)$

$\begin{vmatrix} -1 &3 &-1 &0 &\cdots &0 &0 &0 &0\\ 0 &-1 &3 &-1 &\cdots &0 &0 &0 &0\\ 0 &0 &-1 &3 &\cdots &0 &0 &0 &0\\ 0 &0 &0 &-1 &\cdots &0 &0 &0 &0\\ \vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots &\vdots &\vdots\\ 0 &0 &0 &0 &\cdots &3 &-1 &0 &0\\ 0 &0 &0 &0 &\cdots &-1 &3 &-1 &0\\ 0 &0 &0 &0 &\cdots &0 &-1 &3 &-1\\ 0 &0 &0 &0 &\cdots &0 &0 &f &g\\ 0 &0 &0 &0 &\cdots &0 &0 &h &i \end{vmatrix}$

用倒数第二行来消倒数第一行，得：

$\begin{matrix} 0 &0 &0 &0 &\cdots &0 &0 &0 &i-g\cdot \frac hf ) \end{matrix}$

现在这个行列式已经是三角行列式了，它的值就是对角线元素之积。
于是：$B =(-1)\times (-1)\times (-1)\times \cdots\times f(i-g\cdot \frac hf )$
一共有 $n-2$ 个 $-1$
如前文所述：$A=(-1)^{n-1}B$
又因为：$B=(-1)^{n-2}(f\cdot i-g\cdot h)$
于是有：$A=(-1)^{2n-3}(f\cdot i-g\cdot h)=-f\cdot i+g\cdot h$

带入 $f$、$g$、$h$、$i$ 的值得：
$A=-(F(n-1)-1)(I(n-1)-1)+(G(n-1)+3)H(n-1)$
带入 $H$、$I$ 的值：
$A=-(F(n-1)-1)(-H(n-2)-1)+(-F(n-2)+3)H(n-1)$
然后再展开……回忆下 $F$、$H$ 的递推式

$\begin{align*} A&=F(n-1)H(n-2)+F(n-1)-H(n-2)-1-F(n-2)H(n-1)+3H(n-1)\\ &=H(n)+F(n-1)+F(n-1)H(n-2)-F(n-2)H(n-1)-1\\ &=H(n)+F(n-1)+\begin{vmatrix}F(n-1) &H(n-1)\\F(n-2) &H(n-2)\end{vmatrix}-1 \end{align*}$

发现不能化简了？
没关系！在行列式上动动手脚吧！

FH 定理

对于任意大于 $2$ 的 $k$ 有：

$\begin{vmatrix} F(k-1) &H(k-1)\\ F(k-2) &H(k-2) \end{vmatrix}=\begin{vmatrix} F(2) &H(2)\\ F(1) &H(1) \end{vmatrix}$

证明：
对于行列式：$\begin{vmatrix} F(k-1) &H(k-1)\\ F(k-2) &H(k - 2) \end{vmatrix}$
把行列式最下面的行取反，则行列式的值取反： $-\begin{vmatrix} F(k-1) &H(k-1)\\ -F(k-2) &-H(k-2) \end{vmatrix}$
把行列式的上面的行乘以 $3$ 加到下面去： $-\begin{vmatrix} F(k-1) &H(k-1)\\ 3F(k-1)-F(k-2) &3H(k-1)-H(k-2) \end{vmatrix}$
特意构造的递推式出现了： $-\begin{vmatrix} F(k-1) &H(k-1)\\ F(k) &H(k) \end{vmatrix}$
有点眉目了~ 把第一行与第二行调换位置，行列式的值取反： $\begin{vmatrix} F(k) &H(k)\\ F(k-1) &H(k-1) \end{vmatrix}$
一目了然，这是 k++ 后的行列式的样子。（ pascal同学早日转C++ ）
那么立即推出： $\begin{vmatrix} F(k-1) &H(k-1)\\ F(k-2) &H(k-2) \end{vmatrix}=\begin{vmatrix} F(2) &H(2)\\ F(1) &H(1) \end{vmatrix}$
FH 定理得证。

利用 FH 定理，把 $F(1)=-1,F(2)=-3,H(1)=3,H(2)=8$带入： $\begin{vmatrix} F(n-1) &H(n-1)\\ F(n-2) &H(n-2) \end{vmatrix}=-1$

于是就爽了嘛！

$\begin{align*} \therefore A&=H(n)+F(n-1)+(-1)-1\\ &=H(n)+F(n-1)-2 \end{align*}$

进一步我们发现……
设 $R(n)=H(n)+F(n-1)-2$
那么立即有：

$\begin{align*} R(n)&=3H(n-1)-H(n-2)+3F(n-2)-F(n-3)-2\\ &= 3(R(n-1)+2)-(R(n-2)+2)-2\\ &= 3R(n-1)-R(n-2)+2 \end{align*}$

所以，轮状病毒的方案数满足递推式 $F(n)=3F(n-1)-F(n-2)+2$ ，其中 $F(1)=1,F(2)=5$
然后随手写一个高精度就可以过了～

法二：DP

转载自 boshi
如果用 $f[x]$ 表示加入了 $x$ 个周围的点后的方案数，我们首先想到的递推式是：$f[i]=\sum_{j=1}^i f[i-j]\cdot j$
解释：最后加入的 $j$ 个点每个都可能与中心点连边，将所有方案数累加即可。
但是，第一个点永远不会与第 $n$ 个点连边，因此方案数统计并不准确。
我们再设：$g[i]=\sum_{j=2}^i f[i-j]\cdot j\cdot (j-1)$
解释：如果有 $j$ 个周围的点连成一条，且跨越了 $1$ 和 $n$，我们将所有这样的情况累加到答案中去。如果这样的点有 $j$ 个，剩下的点肯定不与这 $j$ 个点相连，所以连边方案数就是 $f[i-j]$，这 $j$ 个点有 $(j-1)$ 种选法(跨越 $1$ 和 $n$ )，与中心点连边的方案数是 $j$ ，根据乘法原理，答案要累加 $f[i-j]\cdot j\cdot (j-1)$ 。
这样的 f[n]+g[n] 就是我们要求的轮状病毒的数量。

下面我们思考如何快速求出 $f$ 和 $g$。

多阶差分

首先分析 $f[i]$。如果我们可以求出所有 $f[i-j]\cdot j$ 的前缀和，这个问题就变得非常方便了。问题是对于不同的 $i$，这个前缀和中每一项都会发生变化。
那如果我们知道了变化的量是多少呢？于是我们就对前缀和进行差分。

$\begin{align*} \Delta f[i]&=\sum_{j=1}^i f[i-j]\cdot j - \sum_{j=1}^{i-1} f[i-1-j]\cdot j\\ &=\sum_{j=0}^i f[i-j]\cdot j - \sum_{j=0}^{i-1} f[i-1-j]\cdot j\qquad (f[i]\cdot 0=f[i-1]\cdot 0=0)\\ &=\sum_{j=0}^i f[j]\cdot (i-j) - \sum_{j=0}^{i-1} f[j]\cdot (i-1-j)\qquad (\text{交换枚举顺序})\\ &=\sum_{j=0}^i f[i]\\ g[i]&=\sum_{j=2}^i f[i-j]\cdot j \cdot (j-1)\\ &=\sum_{j=0}^i f[i-j]\cdot j \cdot (j-1)\qquad(f[i-1]\cdot 1\cdot 0=0)\\ \Delta g[i]&=\sum_{j=0}^i f[i-j]\cdot j \cdot (j-1)-\sum_{j=0}^{i-1} f[i-j-1]\cdot (j-1) \cdot (j-2)\\ &=\sum_{j=0}^i f[j]\cdot (i-j)\cdot (i-j+1)-\sum_{j=0}^{i-1} f[j]\cdot (i-j)\cdot (i-j-1)\\ &=\sum_{j=0}^i f[j]\cdot (i-j)\cdot 2\qquad(i-i=0)\\ \Delta^2 g[i]&= \sum_{j=0}^i f[j]\cdot (i-j)\cdot 2-\sum_{j=0}^{i-1} f[j]\cdot (i-j-1)\cdot 2\\ &=\sum_{j=0}^i 2f[j]\qquad(i-i=0)\\ \therefore \Delta^3 &=2f[i] \end{align*}$

我们维护 $f[i]$ 的前缀和，以及 $f[i-j]\cdot j$ 的前缀和，每次将 $f[i]$ 累加进 $f[i]$ 的前缀和，将 $f[i]$ 的前缀和累加进 $f[i-j]\cdot j$ 的前缀和，$g[i]$ 同理

行列式解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define digit 100000000
using namespace std;
struct bigint
{
	mutable int a[205];
	inline bigint()
	{
		memset(a,0,sizeof(a));
		a[0]=1;a[1]=0;return;
	}
	inline bigint(int b)
	{
		memset(a,0,sizeof(a));
		a[0]=1;a[1]=b;return;
	}
	inline int& operator[](size_t pos)const{return a[pos];}
	inline bigint operator+(int b)const
	{
		int i;bigint c=*this;
		c[1]+=b;
		for(i=1;i<=c[0];++i)
		{
			if(c[i]>=digit)
			{
				++c[i+1];c[i]-=digit;
			}
		}
		if(c[c[0]+1])++c[0];
		return c;
	}
	inline bigint operator-(const bigint& b)const
	{
		int i;bigint c;c[0]=a[0];
		for(i=1;i<=c[0];++i)c[i]=a[i]-b[i];
		for(i=1;i<=c[0];++i)
		{
			if(c[i]<0)
			{
				c[i]+=digit;--c[i+1];
			}
		}
		while(!c[c[0]]&&c[0]>1)--c[0];
		return c;
	}
	inline bigint operator*(int b)const
	{
		int i;bigint c;c[0]=a[0];
		for(i=1;i<=c[0];++i)c[i]=a[i]*b;
		for(i=1;i<=c[0]||c[i];++i)
		{
			if(c[i]>=digit)
			{
				c[i+1]+=c[i]/digit;c[i]%=digit;
			}
		}
		c[0]=i-1;
		return c;
	}
	friend ostream& operator<<(ostream& os,const bigint& a)
	{
		printf("%d",a[a[0]]);
		for(int i=a[0]-1;i>=1;--i)printf("%08d",a[i]);
		return os;
	}
}f[3005];
int main(void)
{
	int i,n;
	scanf("%d",&n);
	f[1]=1;f[2]=5;
	for(i=3;i<=n;++i)f[i]=f[i-1]*3-f[i-2]+2;
	cout<<f[n]<<endl;
	return 0;
}

DP解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define digit 1000000000
using namespace std;
struct bigint
{
	mutable int a[205];
	inline bigint()
	{
		memset(a,0,sizeof(a));
		a[0]=1;a[1]=0;return;
	}
	inline bigint(int b)
	{
		memset(a,0,sizeof(a));
		a[0]=1;a[1]=b;return;
	}
	inline int& operator[](size_t pos)const{return a[pos];}
	inline bigint& operator+=(const bigint& b)
	{
		int i;a[0]=max(a[0],b[0]);
		for(i=1;i<=a[0];++i)a[i]+=b[i];
		for(i=1;i<=a[0];++i)
		{
			if(a[i]>=digit)
			{
				++a[i+1];a[i]-=digit;
			}
		}
		if(a[a[0]+1])++a[0];
		return *this;
	}
	friend ostream& operator<<(ostream& os,const bigint& a)
	{
		printf("%d",a[a[0]]);
		for(int i=a[0]-1;i>=1;--i)printf("%09d",a[i]);
		return os;
	}
}F=1,F1=1,F2=1,G=0,G1=0,G2=0;
int main(void)
{
	int i,n;
	scanf("%d",&n);
	for(i=1;i<=n;++i)
	{
		if(i)G2+=F,G2+=F;
		if(i<n)G1+=G2,G+=G1;
		F=F1;F2+=F;F1+=F2;
	}
	cout<<(F+=G)<<endl;
	return 0;
}

完结撒花！★,°:.☆(￣▽￣)/$:.°★